Hva er regresjon?

Mange studenter har glemt hva de lærte om regresjon på videregående skole. Dette innlegget har som hensikt å gi en oppfriskning ved å vise det mest grunnleggende innen regresjon: den lineære funksjonen.

Regresjonskoffisienter er et statistisk mål på forholdet mellom variabler. Når vi beregner regresjonskoffisienter, bruker vi regresjonsanalyse. Det finnes mange forskjellige former for regresjonsanalyse som brukes til mange ulike formål.

Regresjonslinjen

Regresjonsanalyse gir oss en linje som beskriver korrelasjonen mellom våre variabler. Det er denne linjen som er grunnlaget for all regresjonsanalyse.

Den matematiske lineære funksjonen

I matematikken representerer en lineær funksjon en rett linje når den plottes i et koordinatsystem. Den kan beskrives med formelen:

\(Y = a + bX\)

I denne funksjonen indikerer konstantleddet, a, gjennomsnittsverdien av Y når X er lik null. Helningskoffisienten, b, indikerer hvor mye Y i gjennomsnitt øker eller minker for en enhets økning i X.

Når b er større en null er effekten positiv: En økning i X fører til en økning i Y, og en reduksjon i X resulterer i en reduksjon i Y. For eksempel, hvis b er lik 5, øker Y med 5 enheter når X øker med 1 enhet.

Når b er mindre en null, er effekten negativ: Hvis X øker, minker Y, og hvis X minker, øker Y. Hvis, for eksempel, b er lik -2, minker Y med to enheter når X øker med en enhet.

Den statistiske lineære funksjonen

Den statistiske lineære funksjonen, spesifikt innenfor konteksten av enkel lineær regresjon, har en lignende form som den matematiske lineære funksjonen, men tolkningen og konteksten er noe annerledes. Formelen er:

\(Y = β_0 + β_1X + ϵ\)

Her representerer:

\(Y\) er den avhengige variabelen vi ønsker å forklare
\(X\) er den uavhengige variabelen vi bruker for å gjøre forklaringene
\(B_0\) (Beta null) er konstantleddet, eller den forventede verdien av Y når X = 0
\(Β_1\) (Beta en) er helningskoffisienten, eller endringen i Y for en enhetsendring i X.
\(ϵ\) (Epsilon) er en tilfeldig feilterm som fanger opp alle andre faktorer som påvirker Y men som ikke er inkludert i modellen.

Den statistiske lineære funksjonen brukes til å modellere forholdet mellom to variabler ved å tilpasse en lineær funksjon til de obeserverte dataene. Da kan man analysere hvordan endringer i den uavhengige variabelen er assosiert med endringer i den avhengige variabelen.

En lineær funksjon i R

I dette eksempelet vil jeg bruke datasettet ´mtcars´ som kommer forhåndsinstallert i R. Jeg er interessert i å finne ut av hvor mye drivstoff en bil bruker på en gitt avstand (Miles per Gallon) i forhold til dens vekt (Weight).

Jeg har laget en spredningsplott med en lineær regresjonslinje som viser forholdet mellom ´mpg´ (Miles per Gallon) og ´wt´ (bilens vekt i 1000 lbs).

## Linear function in R ##

# Loading package and dataset
library(tidyverse)

# Fitting a linear model
model <- lm(mpg ~ wt, data = mtcars)

# Extracting coefficients
intercept <- round(coef(model)[1], 2)
slope <- round(coef(model)[2], 2)

# Creating the functions string
equation <- paste("mpg = ", intercept, " + ", slope, "*wt")

# The plot
mtcars %>% 
  ggplot(aes(x = wt, y = mpg)) +
  geom_point(color = "black") +
  geom_smooth(method = "lm", color = "red") + 
  labs(x = "Weight (1000 lbs)",
       y = "Miles per Gallon",
       title = "MPG by Weight") +
  annotate("text", x = max(mtcars$wt) * 0.6, y = max(mtcars$mpg) * 0.9,
           label = equation, hjust = 0, color = "black", size = 4) +
  theme_bw()

Ved å kjøre denne koden vil du få denne spredningsplotten.

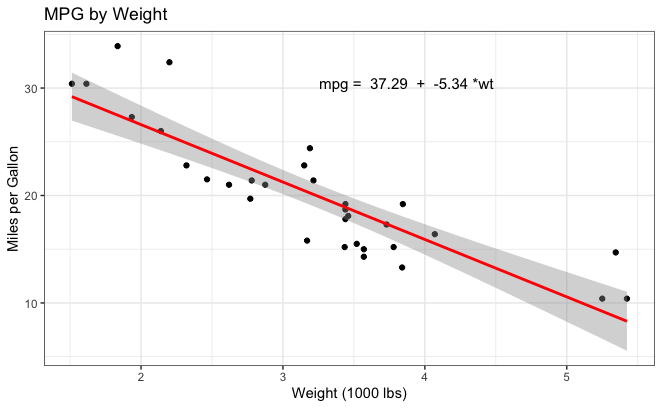
Tolkning

Hvert enkelt punkt i spredningsplottet representerer en bil fra ´mtcars´datasettet. X-aksen viser bilens vekt mens Y-aksen viser bilens drivstoffeffektivitet.

Den røde linjen er et resultat av en lineær regresjonsanalyse. Denne linjen representerer det best passende forholdet mellom bilens vekt og dens drivstoffeffektivitet.

Konstantleddet er 37.29. Den representerer gjennomsnittsverdien av ´mpg´(Miles per Gallon) når ´wt´ (Weight) er lik null. Dette er et teoretisk punkt for i den ekte verden så kan ikke en bil ha null vekt. Likevel så er det viktig for å si noe om den lineære sammenhengen.

Helningskoffisienten er -5.34. Denne verdien sier noe om hvor mye ´mpg´ (Miles per Gallon) er forventet å endre seg i forhold til en enhetsøkning i bilens vekt. En negativ helning som i dette tilfellet, indikerer at dersom vekten økes så vil drivstoffeffektiviteten minke.

Vår lineære regresjonslinje har en negativ helning som indikrerer en negativ korrelasjon mellom bilens vekt og dens drivstoffeffektivitet. Det betyr at tyngre biler har en tendens til å være mindre drivstoffeffektive.

Jo nærmere datapunktene er til den lineære regresjonslinjen jo sterkere er forholdet mellom drivstoffeffektivitet og vekt. Dersom punktene er mer spredt rundt linjen så antyder det at det er andre faktorer som også har innflytelse på bilens drivstoffeffektivitet.

Linear regression - predictive model

Written by Knut Solvig

Denne delen av innlegget skulle egentlig være på norsk, men jeg (Knut) begynte bare å skrive engelsk… beklager ;) Dersom du sliter med å forstå på engelsk kan jeg anbefale nettsiden deepl.com for å oversette. Eventuelt kan du sende oss en e-post på codinghjornet@gmail.com

When dealing with quantitative methods, it can be very relevant to look at predictive models. These models help to “predict” a value based on a coefficient (as obtained through a linear model). The formula for a predictive model is not very complicated:

\(\hat{y} = ax + b\)

Where \(a\) is the slope of the regression (coefficient of independent variable). In turn, \(x\) is the assumed value of the predictor value. Lastly, \(b\) is the intercept for y (dependent variable).

To simplify and understand how this formula works, consider the following minimal example:

library(tidyverse)
weight <- c(50, 60, 70, 80, 90, 50, 60, 75)
height <- c(160, 165, 170, 175, 180, 165, 168, 175)

Here we assign a few values to the new variables weight and height. These values are artificial, only used for this example.

df <- data.frame(height, weight)

model1 <- lm(height ~ weight, data = df)

Next, we assign these variables into a data frame (making it into a dataset). And run the R function lm()and assigning that to model1 to get the regression model for our dependent variable (height) and the independent variable (weight)

summary(model1)


Call:
lm(formula = height ~ weight, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.3002 -1.2759 -0.2516  1.3796  2.6998 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 140.22678    3.39563  41.296 1.35e-08 ***
weight        0.44147    0.04978   8.869 0.000114 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.893 on 6 degrees of freedom
Multiple R-squared:  0.9291,    Adjusted R-squared:  0.9173 
F-statistic: 78.65 on 1 and 6 DF,  p-value: 0.0001144

Now we summarize model1. Here we will get the information we need.

Now, we have everything we need. For this part, you do not need to use R. Get out a calculator.

Recall that the formula goes like this: \(\hat{y} = ax + b\). Our \(a\) in this example is \(0.44147\) because that is the coefficient for weight.

Our formula now then looks like this: \(\hat{y} = 0.44147x + b\)

Next, we plot in the value of \(b\): The Y intercept. In this case, it is \(140.22678\). This means, that if your weight is 0 (quite unrealistic), your height would be 140 according to this model. Our formula now looks different: \(\hat{y} = 0.44147x + 140.22678\)

Now, we are ready to predict.

Currently, our formula is not giving any results, because we haven’t input a value yet.

Let’s say we would like to check how tall a person that weighs 68kg would be. We then have to type this into a calculator: \(0.44147*(68)+140.22678\). This gives us the result: \(170.24674\) or \(170\) centimeters if we round down. This model can then be used for any values we wish.

Any more questions after reading this blog post? Feel free to e-mail us at codinghjornet@gmail.com. We answer e-emails whenever we can, during our work hours.